[12] YardSweeper

wilkopolis
May 4
12 min read

As a side project, I made a free game for android/windows and a paid game for iOS - check it out here.

The rest of this post will be a long journal about this project's history up until release (and a secret advanced strategy tip at the end).

Conception

Earlier this year a friend and I were enjoying his playthrough of a pokemon romhack, when we got to the games corner. This romhack included (for completeness or fun) voltorb flip, a minigame I thoroughly enjoyed back in the day.

The game is a variation of picross with voltorbs (mines). The board is made up of hidden tiles, and you are given the count of mines and the sum of all values in that row/column. Your goal being to expose all the 2s and 3s.

This game is really fun, and very challenging for those who enjoy logic puzzles. Its critical flaw (in my opinion) is that sometimes it requires you to guess-which is antithetical to logic puzzles.

I had just hit a milestone in Death&Tactics development, and decided to take a detour and try to make a version of voltorb flip myself. Shouldn't take that long, right?

My goal was to tweak the gameplay to be unique/distinct, re-theme the game to something original, and above all else-remove any guesswork.

Early Attempts

Before worrying about the look and feel, my first goal was to come up with a twist on the original gameplay.

At first I generated the same type of boards, but added gravestones. The gravestone would show the sum of total loot in that grave. In the below screenshots however, there is no indication of the shape/size of the grave.

After I found this game still had the same "guessing" issue, I added more board information-a loot tracker that told you the contents of the board (didn't solve it either).

After the first round of attempts: I considered the idea of splitting the board into sections. I felt this breakup was a fun aesthetic improvement. I enjoyed the idea of the board being make of many small plots or sections. After working on a macabre game for 5+ years, I naturally related this setup to a scrambled graveyard.

Despite still being a visual mess, I continued trying to refine this formula with more tweaks.

I tried displaying the "amount of loot visible from standing at this spot and looking into the row or column, until you hit something that wasn't loot"-don't know how to more concisely phrase that. Didn't work.

After some more refinement, I moved forward with a design and tried to polish it up-so I could share it with friends.

Using art I had laying around (and some amateur ms paint work), I threw together a demo with a new tool: the probe.

The probe was my early attempt to try to solve the "guessing" problem. This tool would allow players to see what was under a tile without digging it up. Probe charges would be limited each level. In theory this could be a thematic/interactive way to solve the lack of information.

Probe values would show up on the little screen, and probe charges were scattered throughout the board.

Ultimately this was not a precise enough solution. There was no correlation with board generation parameters and the amount of probes needed.

Also, I felt like the game was best when it was most simple. I wanted this to be a puzzle game like Sudoku. Additional rules and tools and mechanics would be less appealing to the casual puzzle gamer. Not that it wasn't fun to others. I decided to scrap the probe system and try to approach boards in another way.

The next section is going to describe the unique programming challenges. It deals with trying to remove ambiguous boards with multiple solutions, and trying to make this game a fully deductible logic puzzle.

"Luck" a.k.a. Cycles

This may be the trickiest thing I've ever had to program. Not necessarily due to difficult bugs, or a complex design-but it required a lot of engineering to get running fast enough to play. The goal was clear: make it so that you can solve all these boards without guessing. I'll describe the program in a bit more detail later.

After playing with the different board rules, I settled on the final design that exists today:

Loot tracker showing the occurrence of each value in the board.
Row/Column with mine/loot totals.
Sudoku rules where values can not overlap.
Veins which have 0 value, but are safe to dig.

These rules are not perfect however. Board generation can create boards with multiple mine arrangements, that fit within those rules. Here is the simplest example:

If you look at the original, you may be able to tell that you do not have enough information to solve. This is because there are multiple places the mines (skulls) can be. Because of this you can not win with deduction alone, you would have to guess.

Potentially there may be a different set of rules where board generation is quick, fun, original, and required no guessing-I did not find one.

The word I use to describe subsections of the board where you would have to guess, is a "cycle". Something about the constraints of the board being too vague, and the solutions being re-arrangements of the same original values-it seemed appropriate.

From this point on, I was now attempting to detect all cycles. The above example is a pattern that exists for any 4 tile arrangement within 2 parallel graves.

board 1/2:
 2,-,2
[2,-,O] 2
[-,-,-] -
[O,-,2] 2

board 2/2:
 2,-,2
[0,-,2] 2
[-,-,-] -
[2,-,0] 2

If you are thinking ahead, you may be wondering what are the types of cycles-is that the only one? It turns out I could not figure out a general solution-but there are many more. I was able to take the problem much further, and eventually shipped a playable game.

In order to tackle this problem, I wrote a brute-forcer that would generate every possible board of size N.

The program would generate every board of size N, of only parallel graves, and look for different arrangements that would fit under the same constraints. The boards had to follow the original Sudoku rules as well. But as board sizes grows, the resources required grew very quickly.

Boards sized 2 took <1 second to run.
Boards sized 3 took about 12 seconds to run.
Boards sized 4 took about 72 minutes to run.

I started running the program for size 5, but the memory used to store boards (very simple data structures, with maybe only a few KB of information) grew to 20+ GB of RAM usage in about 10 seconds-at that point I pulled the plug.

You may be able to tell from the runtime that running this for board size 5 may have taken longer than 24 hours. Either way, I figured to try to solve it with the data I had.

Here are some cycles for board size 3 and 4.

Board size 3

 4,4,4      4,4,4
[1,3,O] 4  [3,1,O] 4
[3,O,1] 4  [1,O,3] 4
[O,1,3] 4  [O,3,1] 4

Board size 4

 8,8,8,8      8,8,8,8
[1,3,4,O] 8  [1,3,4,O] 8
[3,1,O,4] 8  [3,1,O,4] 8
[4,O,1,3] 8  [4,O,3,1] 8
[O,4,3,1] 8  [O,4,1,3] 8

And those are just the simple cycles. Eagle eyed readers may see a simple pattern: N mines and N of the same value for an NxN board is always a cycle.

Turns out cycles can exist in other ways. Here is a 3x3 board with 3 skulls and two 1s, two 2s and two 3s. Similar 4x4 board.

 4,5,3         4,5,3
[3,2,O] 5     [3,2,0] 5
[O,3,1] 4     [0,3,1] 4
[1,O,2] 3     [1,0,2] 3

 6,8,7,9       6,8,7,9
[1,3,4,O] 8   [3,1,4,O] 8
[3,4,O,2] 9   [2,4,O,3] 9
[2,O,1,4] 7   [1,O,2,4] 7
[O,1,2,3] 6   [O,3,1,2] 6

That's not all either, due to board generation boards can have irregular shapes.

 4,9,6,5      4,9,6,5
[3,4,2,O] 9  [3,O,2,4] 9
[1,2,O,-] 3  [O,2,1,-] 3
[O,3,1,4] 8  [1,4,3,O] 8
[-,O,3,1] 4  [-,3,O,1] 4

In the end I could not find a general solution. I tried accounting for the number of tiles, the dimension of the board, the rank of occurrences-all to no success. I fumbled around with linear algebra but couldn't get anywhere on my own. I reached out and asked the mathematics discord for some help. I even spent time to make an eye-catching infographic:

One user suggested this is an NP-Hard problem. Could be, I'm no expert. But another user immediately identified this as a use case for an "SAT solver". Having no idea what that was, I googled it and found a set of computational tools for solving combinatorics problems: https://developers.google.com/optimization

ORTools

These are really interesting tools. They computationally solve many classic computing problems such as N-Queens, scheduling and all the ones with knapsacks. I learned there's even an entire software industry for constraint programming. Definitely worth reading up on if you are curious (they have extensive examples and documentation).

I spent a week or so trying to get these to work for YardSweeper, using their documentation and about 30 stack overflow questions (which all of them seem to be answered by the same guy. I think hes the google engineer who maintains the software). After sweating it out for a few days, I was able to model the boards using ORTools. To my disappointment however, this did not yield any time savings.

Not that these tools aren't very advanced (they compete in international integer constraint programming competitions every year https://www.minizinc.org/challenge/2024/results/), but my bespoke solution was running quicker. Either due to my poor application of the tools, or the ability to specifically tailor my solution to the game's rules in ways the more general tools couldn't-I was stuck with my board solver.

Also making my solver multi-threaded made it 4x faster than my original implementation.

Conclusion

To summarize weeks of work, and elide over the rest of the optimizations-I came up with an algorithm to make sure generated boards were playable.

1) Generate a board

2) Build a data structure to represent potential cycles

3) Use derived optimizations, remove all invalid patterns, leaving the smallest dataset possible

4) Brute force the remaining values, to see if there is any cycle. (Look at all arrangements of the remaining values to see if there are more than 1 solution)

The result ended up being something that runs well enough to play. On my hardware, boards can be generated in around a second. With the largest, most difficult boards taking up to a few minutes to generate. I ended up hiding this by generating them in the background while the game runs-and making sure there is a buffer of boards ready for the player.

Android

While it was not my original intention to make it available for android (let alone iOS), it seemed to be a natural fit. Unfortunately, people just don't want to play a minesweeper/sudoku clone on their PC. I would have to make it for phones (or web) if I wanted people to play it. And due to the heavy running board generation, making it web based would be out of the question (without setting up servers and additional infrastructure).

Godot

Despite being Monogame's biggest fan, I was skeptical of porting the game to Android. After a few days of research, the monogame-android community and documentation seemed sparse, and I've never made an Android/iOS app.

Turns out there are seriously many Android/iOS game engines, many of which I've never heard of. Google even recommends a few on their Android documentation:

https://developer.android.com/games/engines/engines-overview

(I think I used Defold in college like 10 years ago. But all that knowledge has left me)

Looking for something a bit more user friendly, and going on name recognition alone, I ended up choosing Godot.

Godot Mobile UI

Development was tricky. I spent a lot of time wrangling with Godot's UI/anchor/layout system. It has all the tools, but its not easy to make a portrait/landscape UI that works on multiple resolutions. Which is a daunting first project (Not to mention all the iOS specific stuff I had to do. You can read more about that in a future post).

There's a post I read which recommended using a square aspect ratio, which makes multiple resolution UI's easier. I will probably check that out for future projects, as I definitely want to make more mobile games.

Godot Android Optimization

After getting the UI working, my one friend (shout out Matt) was reporting very sluggish performance on his device. On all other devices tested, I never had any reports of FPS issues-but I figured it needed to be investigated.

The way the board was originally setup in Godot used controls with lots of child textures. This ran with no issue in my Monogame implementation, but there is one thing I'm omitting here. I was using shaders to color all the grass textures, and corner radii on panel containers for each tile (which was probably another shader).

These shaders ran every frame, even though they only needed to render out the texture once. There was probably a way to bake the shadered textures in Godot-but the more robust way was to just use a spritesheet.

Using Monogame, I rendered out every possible tile into one big texture. Then using basic 2D texture drawing tools in Godot, I was able to get the specific rectangle for any tile I needed to draw. In the end, this brought my average frame time from ~12ms down to ~3ms. You can read a little more detail here: https://forum.godotengine.org/t/trying-to-improve-performance-of-2d-game-on-android/108481/7

Publishing

Just want to say app stores are pretty rigorous about what gets upload these days. Apple requires you to pay $100 a year and build exclusively from their hardware, while Google requires you to have 12 friends for 14 days. Can't say which is harder.

In Conclusion

I'm proud of this game. It was many small, unique, 5-day challenges.
I got to solve some hard programming/math problems.
I gave myself a crash course in Android and iOS development/publishing.
I want to make more mobile games, but I have to finish my PC game first.

Secret advanced tip:

In YardSweeper, I state "Each board has only one solution". But boards don't really have only one solution, I just discard the ones with cycles. The unintended magic recipe to YardSweeper is that you-the player-figure out the unwritten rules while you play. From simple tricks like knowing where the mines aren't, to more complicated boards that require Sudoku rules.

The one most-devious rule, which I describe as "All boards have only one solution" is that boards with cycles are thrown out during generation. This means certain patterns of tiles can not exist.

I believe this rule is required to solve some boards. This is not a rule that I expect most players to figure out. I am, however, calling it fair game. Here an example of the rule in action:

I encountered this board organically while testing. If you want, go and try to solve it yourself. Bring it into paint and scribble down the values. Its very tricky, and I don't think it can be solved without the following knowledge.

I note down all the potential values. Using the loot tracker, grave totals, and Sudoku rules-I believe this is as far as you can take this board.

Then I start with the simplest grave, one that has only two possible configurations. The unknown tiles are either 2 + Skull or Skull + 2. I decide to see if the arrangement of 2 + Skull is correct.

Because of the placement of the 2, I know the other tile must be a skull. And because of this complete grave, I can deduce some other values.
At this point, it seems like we're at another crossroads. However, placing the below skull would cause a cycle. And because I am saying cycles cannot exist, this below board is invalid.
Therefore, the bottom orange grave can only be filled out like this:

Next, I know where a 1 has to be in the green grave:

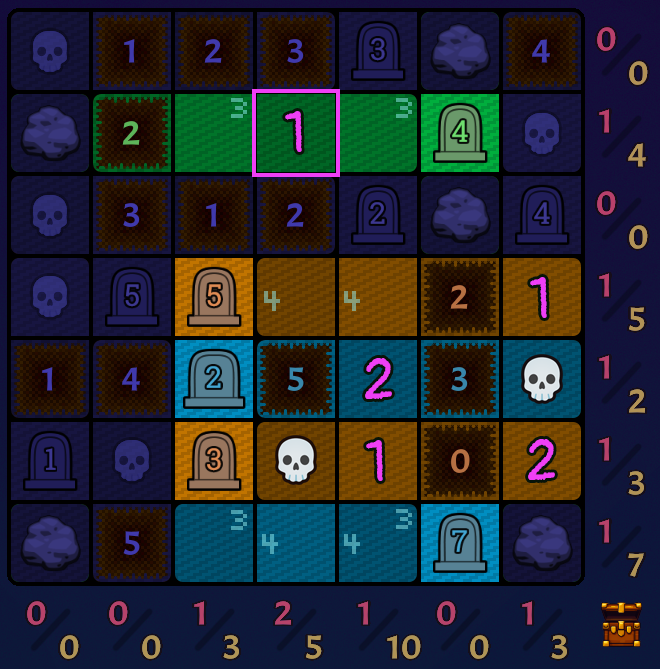
Underneath that 1 I just placed, that column is either 1, 4, Skull, or 1, Skull, 4. The first solution is invalid however, because that order of values would result in another cycle.

Because that board is invalid, I end that timeline and start down the other path-1, Skull, 4.

Up until this point, we have only made 1 assumption: the location of the original 2 in that middle cyan grave. The rest of the values we have placed using logic and rules. This now leaves us at the end of this timeline. The only remaining tiles are that familiar square pattern, with two Skulls and two 3's.

We now know this entire board timeline is impossible. If we follow the timeline where we place that original 2, it leads us to a board that cannot exist. This must mean we can now solve that middle cyan grave, and progress from there.

This must be the values of this grave. Following that we know where the other 2 is.

To avoid a cycle, the Skull in the right-most column must be up in the upper orange grave.
Next, we can now fill out the bottom orange grave.

We can now solve the other orange grave. This is because we know the below board would be invalid.

This would give the following board state

From here we can place the final 4, and the accompanying skull for that bottom cyan grave. This also avoids the original cycle that ended the other timeline.

And with the final 2 tiles (being a 3 and a skull) we can uncover every value on this board!

We may have guessed on a starting point. But we looked at all timelines and proved that there is only one valid solution. All other solutions we tried were dead ends. And this, I believe, is only solvable with the knowledge that cycles can not exist.

The cycles we used to prove out this board were all simple 2x2 cycles. I fear, however, there may be boards that require you to recognize 3x3, or even higher dimension cycles. I have yet to encounter these theoretical boards. But I pray I never do.